Unidade 8 Criação de Gráficos Básicos

O objetivo dessa sessão é a familiarização com os tipos básicos de gráfico que podem ser usados para descrever o comportamento e o relacionamento entre os dados de um estudo estatístico.

8.1 Sumário dos 5 números

O sumário dos 5 números é conhecido como um conjunto de estatísticas descritivas que revelam os percintis gerais mais significativos em uma amostra de dados. Estes são:

1. Mínimo
2. Primeiro quartil
3. Mediana
4. Terceiro quartil
5. Máximo

Por exemplo, em R podemos obter esse sumário por meio do comando summary. Vamos carregar os dados “cars” que apresenta a velocidade e a distância de parada de alguns carros (gravado em 1920!).

help("cars")
data("cars")
summary(cars)

8.2 Importância da visualização dos dados

Apesar das várias medidas estatísticas descritivas disponível, a Figura 8.1 mostra porque a visualização dos dados é muito importante.

Artigo *Same Stats, Diferent Graphs* [@Matejka2017]

Figura 8.1: Artigo Same Stats, Diferent Graphs (Matejka and Fitzmaurice 2017)

8.3 Tipos básicos de gráficos1

Inicialmente, será necessário simular alguns dados para serem usados como fonte na geração de gráficos. Os dados serão armazenados em um data frame contendo 3 variáveis categóricas (fatores em R) e 4 variáveis contínuas.

## Simulando os dados

## 3 variáveis categóricas
FacVar1 = as.factor(rep(c("level1", "level2"), 25))
FacVar2 = as.factor(rep(c("levelA", "levelB", "levelC"), 17)[-51])
FacVar3 = as.factor(rep(c("levelI", "levelII", "levelIII", "levelIV"), 13)[-c(51:52)])

## 4 variáveis númericas
set.seed(123)    # referência para uniformizar as variáveis geradas

NumVar1 = round(rnorm(n = 50, mean = 1000, sd = 50), digits = 2)  ## Distribuição Normal
NumVar2 = round(runif(n = 50, min = 500, max = 1500), digits = 2)  ## Distribuição Uniforme
NumVar3 = round(rexp(n = 50, rate = 0.001))  ## Distribuição exponencial
NumVar4 = 2001:2050

simData = data.frame(FacVar1, FacVar2, FacVar3, NumVar1, NumVar2, NumVar3, NumVar4)

8.4 Uma variávél contínua

8.4.1 Gráfico de pontos (scatter)

plot(simData$NumVar1, type = "o")  ## Index plot

8.4.2 Histograma

hist(simData$NumVar1)  ## histogram

8.4.3 Curva da densidade de probabilidade

plot(density(simData$NumVar1))  ## Kernel density plot

8.4.4 Boxplot

boxplot(simData$NumVar1)  ## box plot

8.5 Variável categórica (ou discreta)

8.5.1 Gráfico de barras (Total)

plot(simData$FacVar3)  ## bar plot

8.6 Duas Variáveis contínuas

plot(simData$NumVar1, type = "o", ylim = c(0, max(simData$NumVar1, simData$NumVar2)))  ## index plot with one variable
lines(simData$NumVar2, type = "o", lty = 2, col = "red")  ## add another variable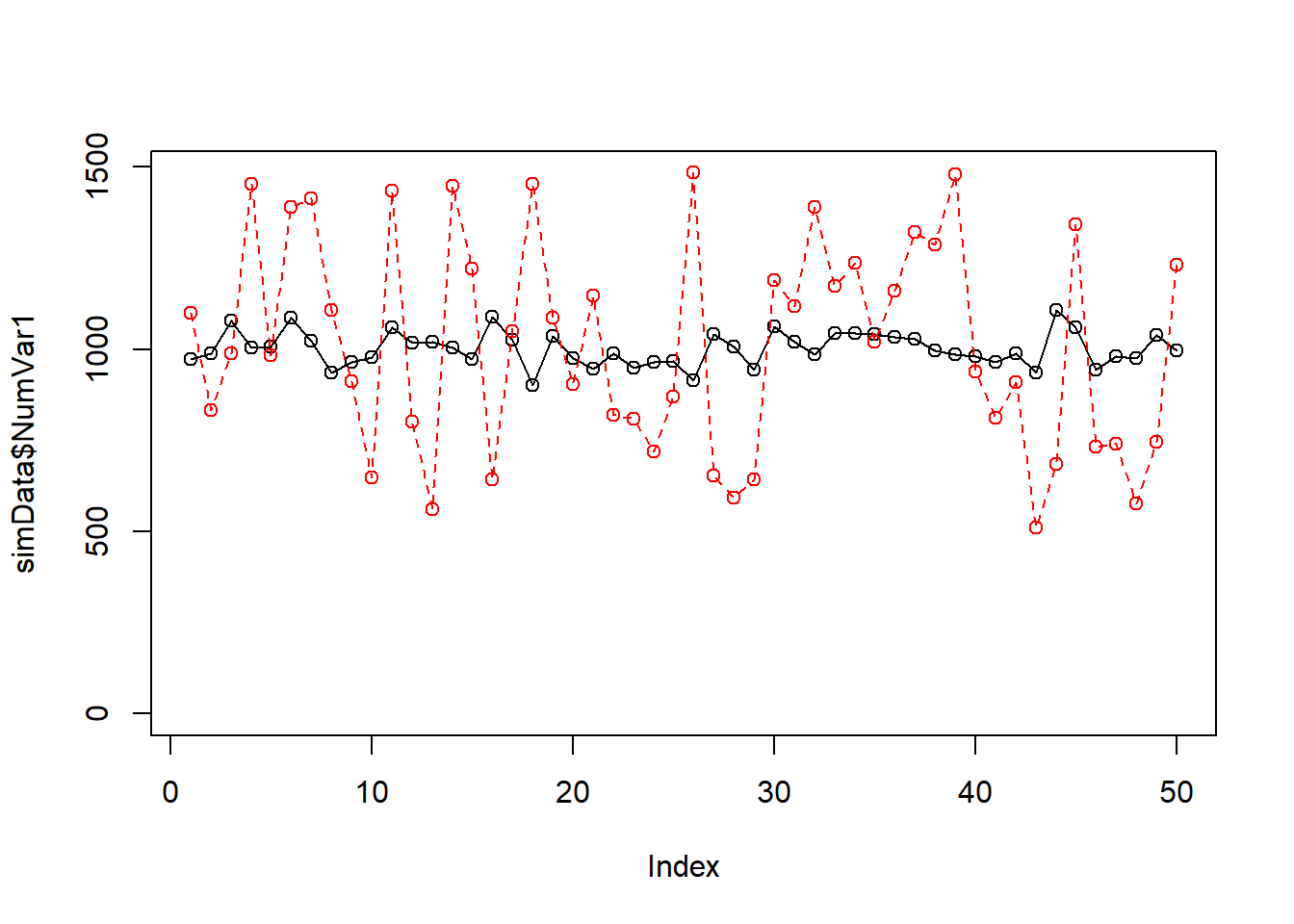

8.6.1 Gráfico de densidade de probabilidade (density plots)

Exemplo de https://stat.ethz.ch/pipermail/r-help/2006-August/111865.html, onde um gráfico “vazio” é produzido e depois preeenchido com linhas (função lines()).

dv1 = density(simData$NumVar1)
dv2 = density(simData$NumVar2)
plot(range(dv1$x, dv2$x), range(dv1$y, dv2$y), type = "n", xlab = "NumVar1(red) and NumVar2 (blue)", 
    ylab = "Density")
lines(dv1, col = "red")
lines(dv2, col = "blue")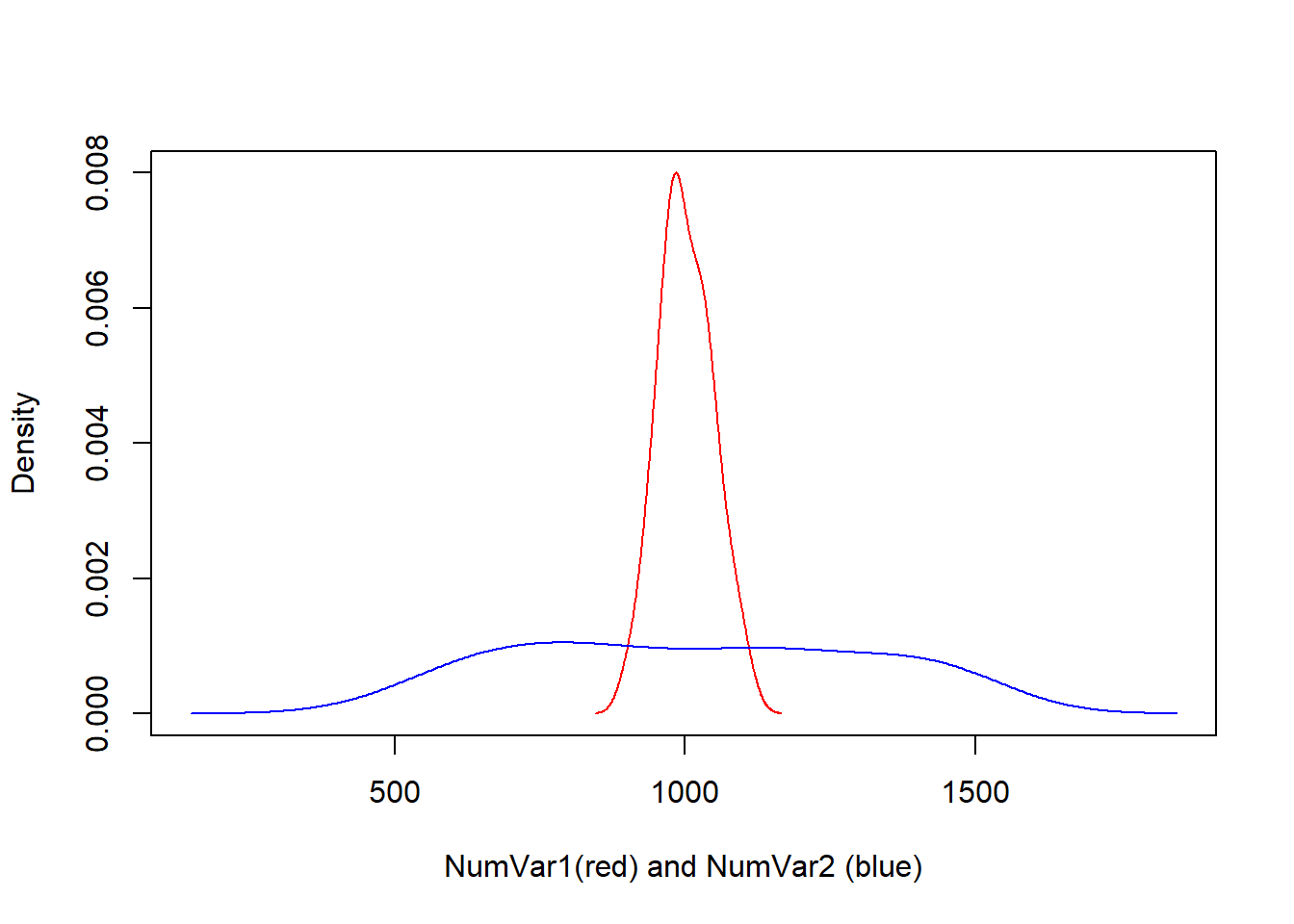

8.6.2 Gráfico de pontos x,y (scatterplots)

plot(simData$NumVar1, simData$NumVar2)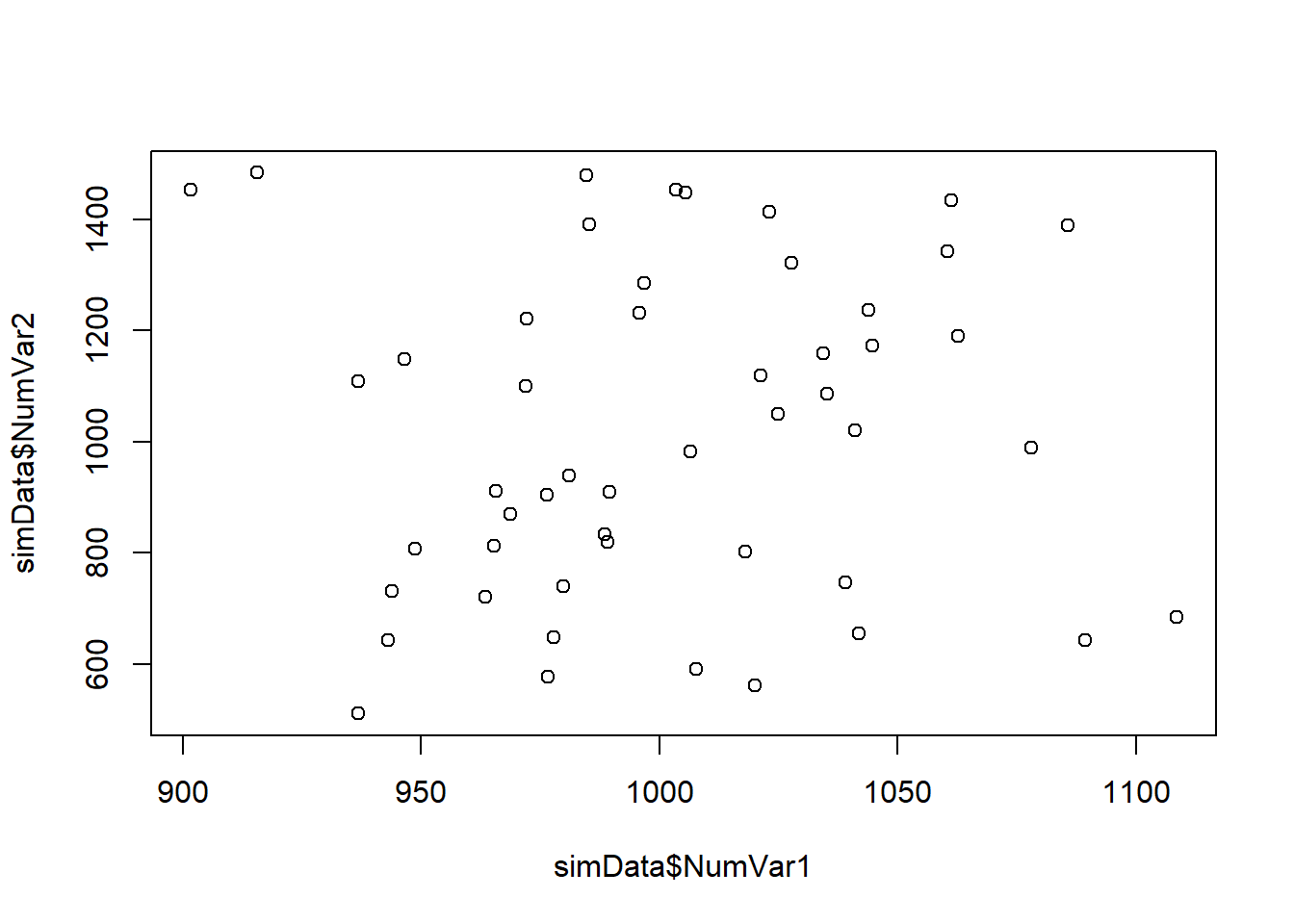

8.7 Duas Variáves categóricas

8.7.1 Mosaico (Mosaic plot)

plot(table(simData$FacVar2, simData$FacVar3))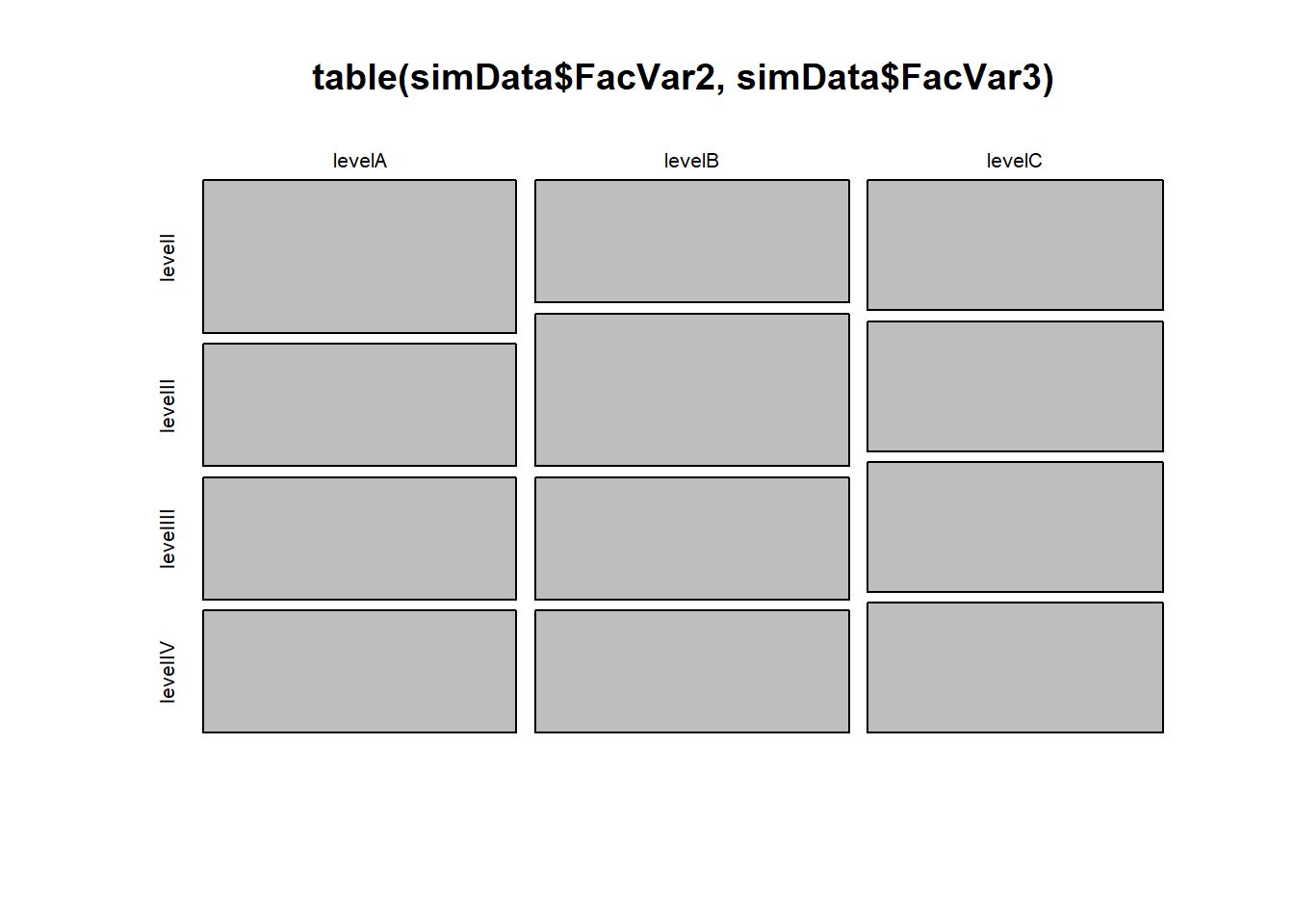

8.7.2 Gráfico de Barras (barplots)

bartable = table(simData$FacVar2, simData$FacVar3)  ## get the cross tab
barplot(bartable, beside = TRUE, legend = levels(unique(simData$FacVar2)))  ## plot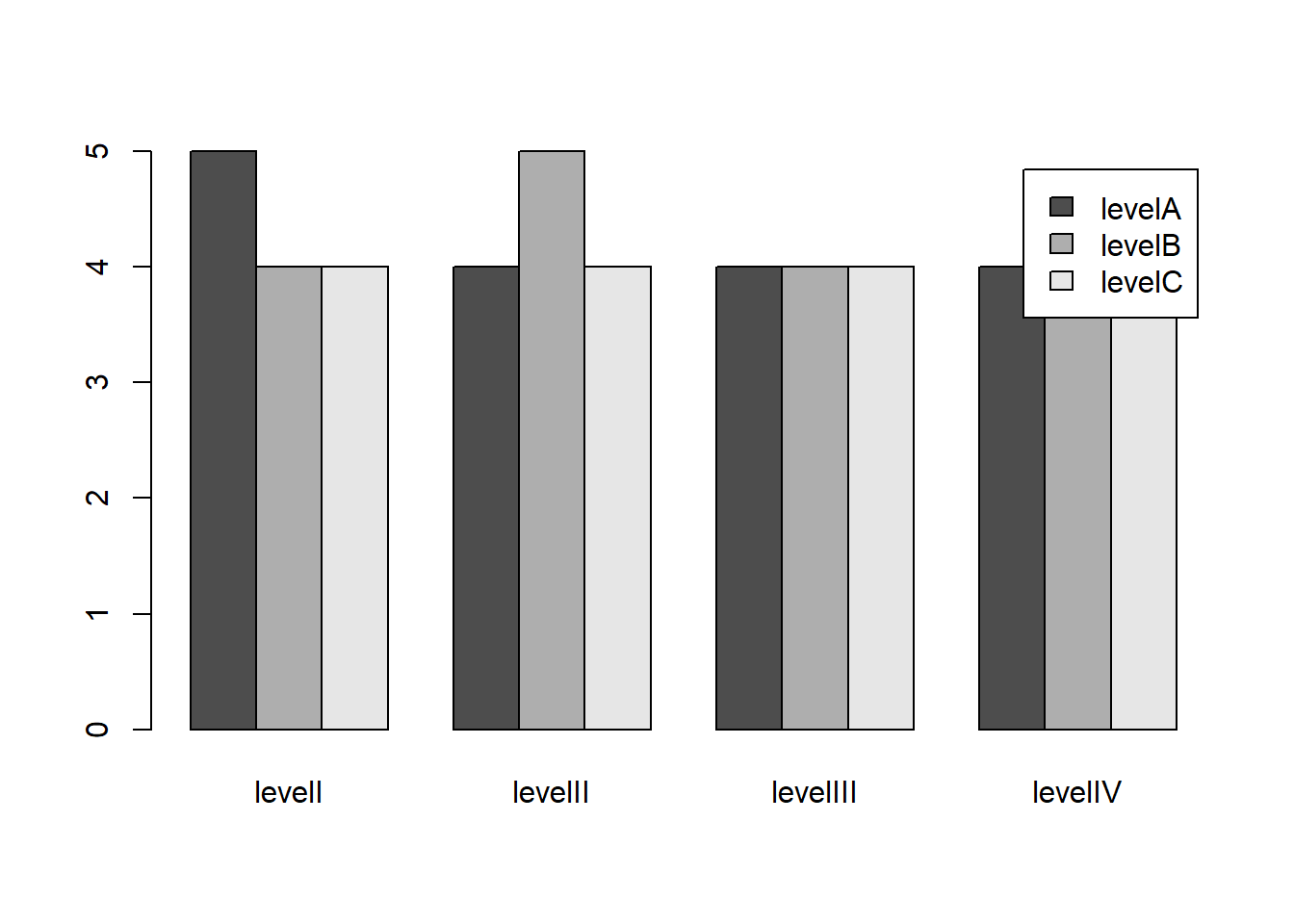

8.7.3 Barras Empillhadas (stacked)

barplot(bartable, legend = levels(unique(simData$FacVar2)))  ## stacked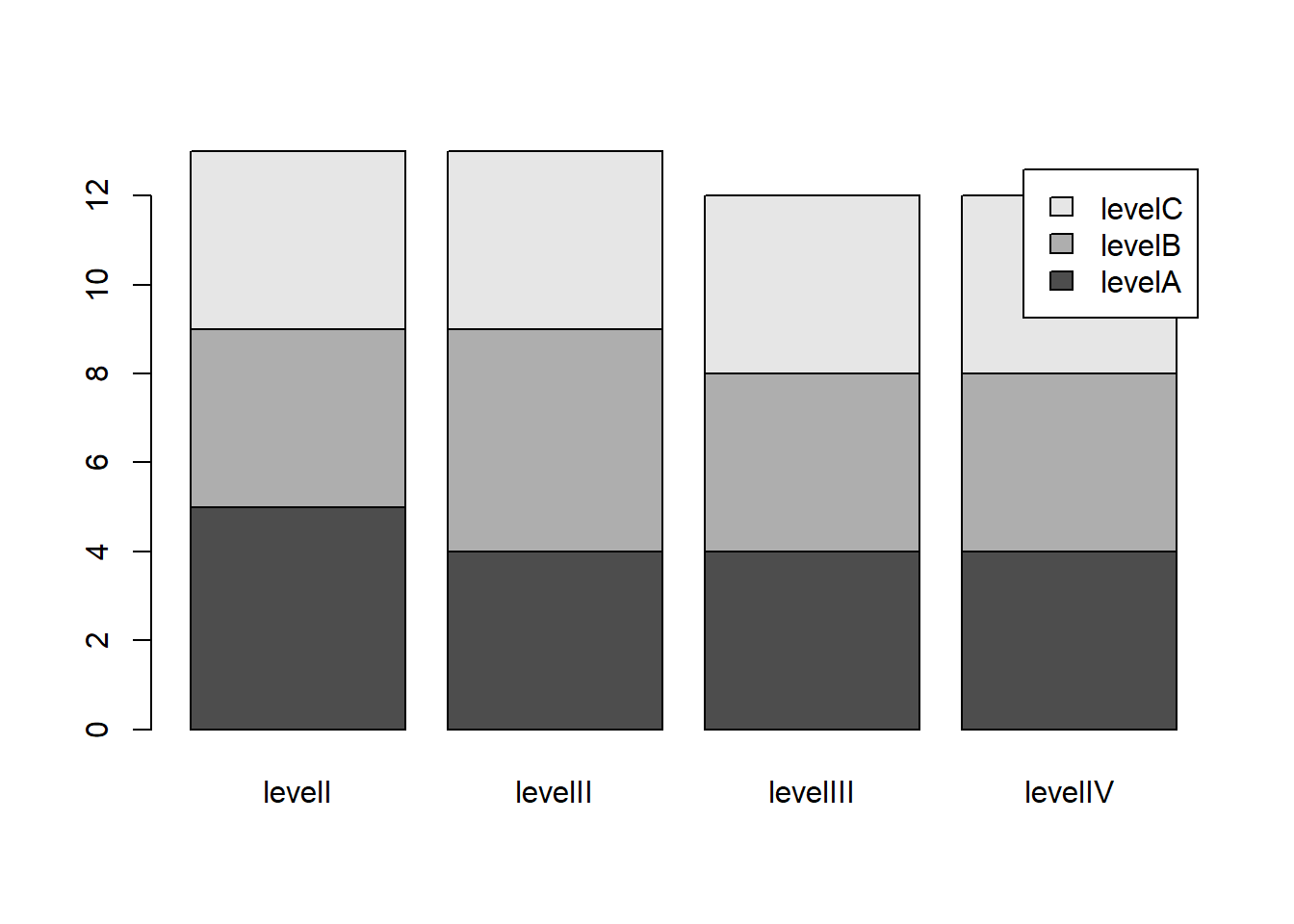

8.7.4 Barras Empillhadas 100% (stacked 100%)

Transformando a tabela para proporções

barplot(prop.table(bartable, 2) * 100,
        legend = levels(unique(simData$FacVar2)))  ## usando prop.table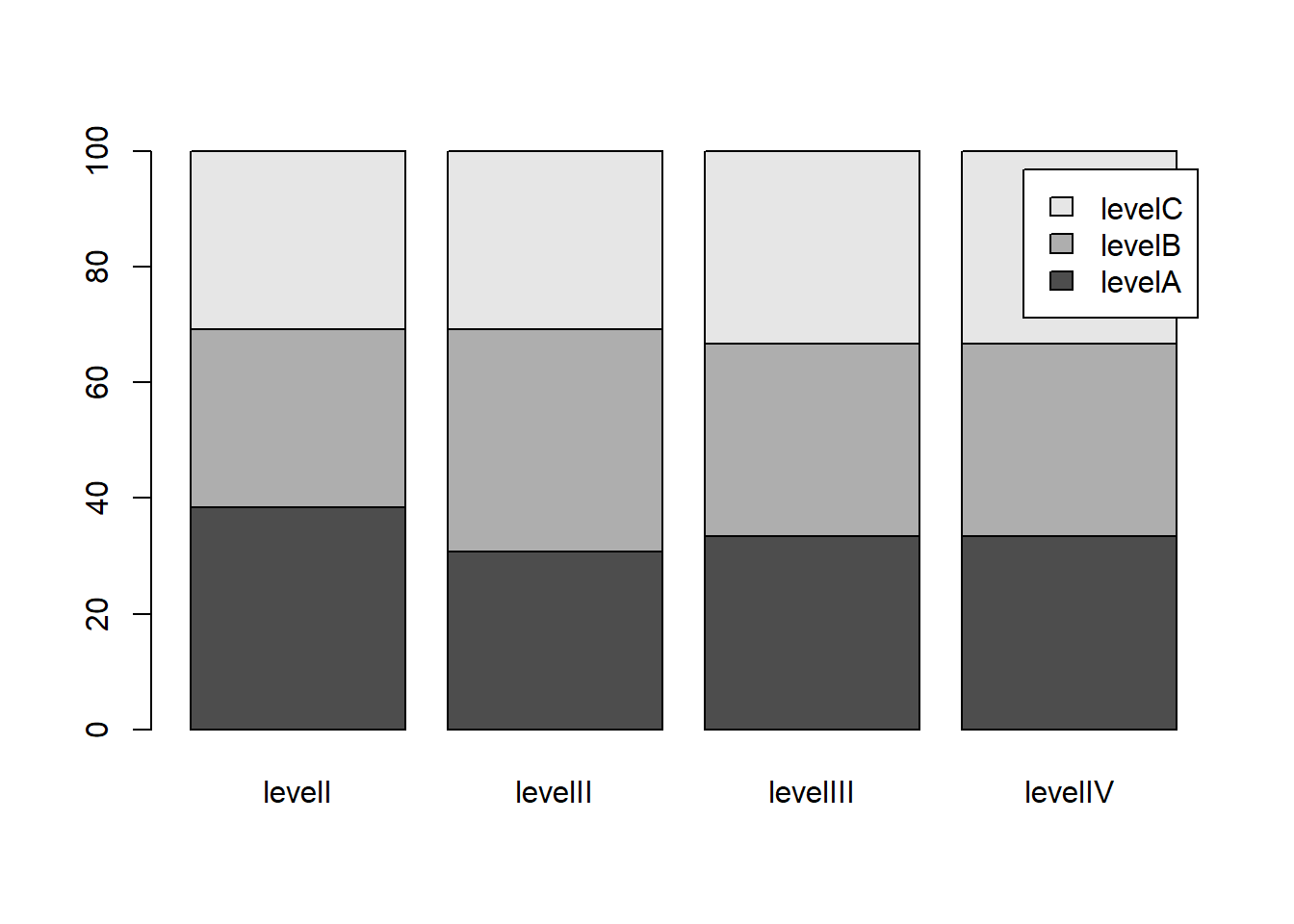

8.8 Duas variáveis: Uma categórica e outra numérica

8.8.1 Box plots: variáveis numéricas por categoria

plot(simData$FacVar1, simData$NumVar1)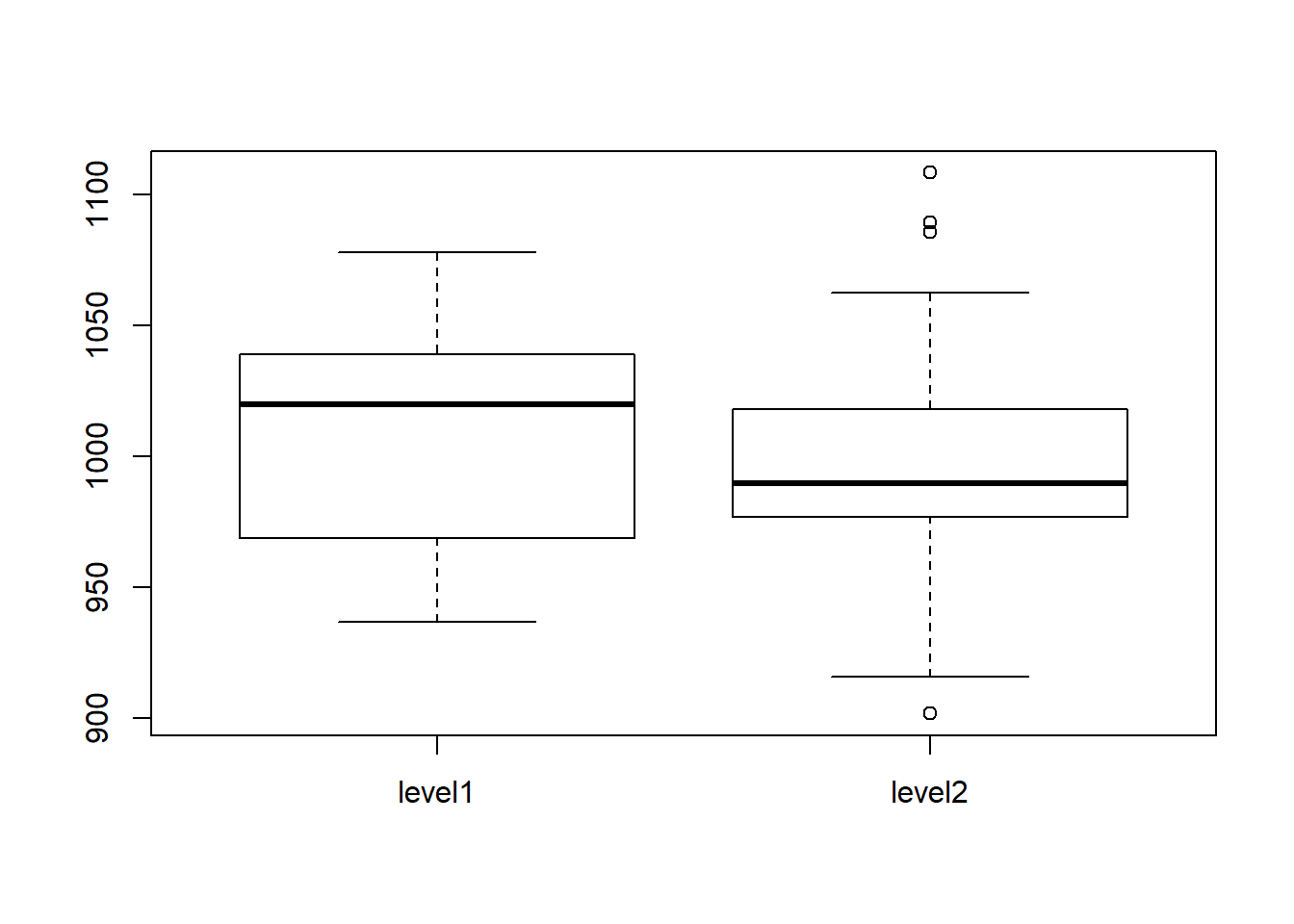

8.8.2 Gráfico de densidade de probabilidade por categoria

level1 = simData[simData$FacVar1 == "level1", ]
level2 = simData[simData$FacVar1 == "level2", ]

dv3 = density(level1$NumVar1)
dv4 = density(level2$NumVar1)

plot(range(dv3$x, dv4$x), range(dv3$y, dv4$y),
     type = "n",
     xlab = "NumVar1 at Level1 (red) and NumVar1 at Level2 (blue)", 
     ylab = "Density")

lines(dv3, col = "red")
lines(dv4, col = "blue")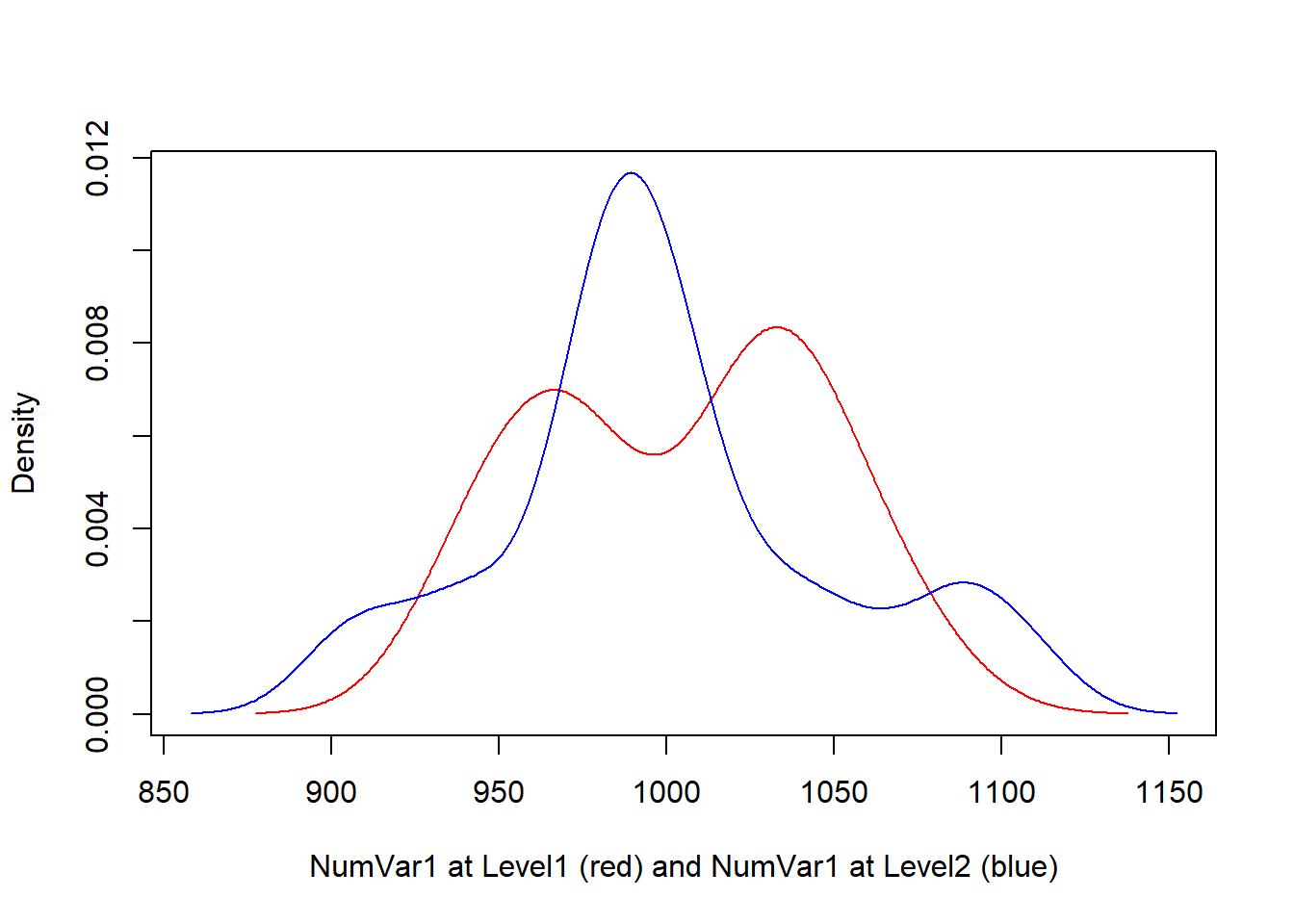

8.8.3 Média de uma variável numérica considerando sua categoria

Verifique como funciona aggregate(), e qual é o retorno de cada função usada como argumento.

list(simData$FacVar3)
aggregate(simData$NumVar1, list(simData$FacVar3), mean)
meanagg = aggregate(simData$NumVar1, list(simData$FacVar3), mean)
meanagg
##    Group.1         x
## 1   levelI  998.8154
## 2  levelII  992.0538
## 3 levelIII 1010.3125
## 4  levelIV 1006.7492
dotchart(meanagg$x, labels = meanagg$Group.1)  ## Dot Chart

Gráfico de barras usando a média

barplot(meanagg$x, names.arg = meanagg$Group.1)  ## Bar plot

Questão: O gráfico anterior é aproproado para comparar as médias (um valor pontual)? Escolha um gráfico melhor :)

8.9 Três variáveis discretas (categorias ou fatores em R)

Arrumando os gráficos matricialmente com a função par()

par(mfrow = c(1, 2))

bar1table = table(level1$FacVar2, level1$FacVar3)
barplot(bar1table, beside = TRUE, main = "FacVar1=level1")

bar2table = table(level2$FacVar2, level2$FacVar3)

barplot(bar2table, beside = TRUE, main = "FacVar1=level2",
        legend = levels(unique(level2$FacVar2)))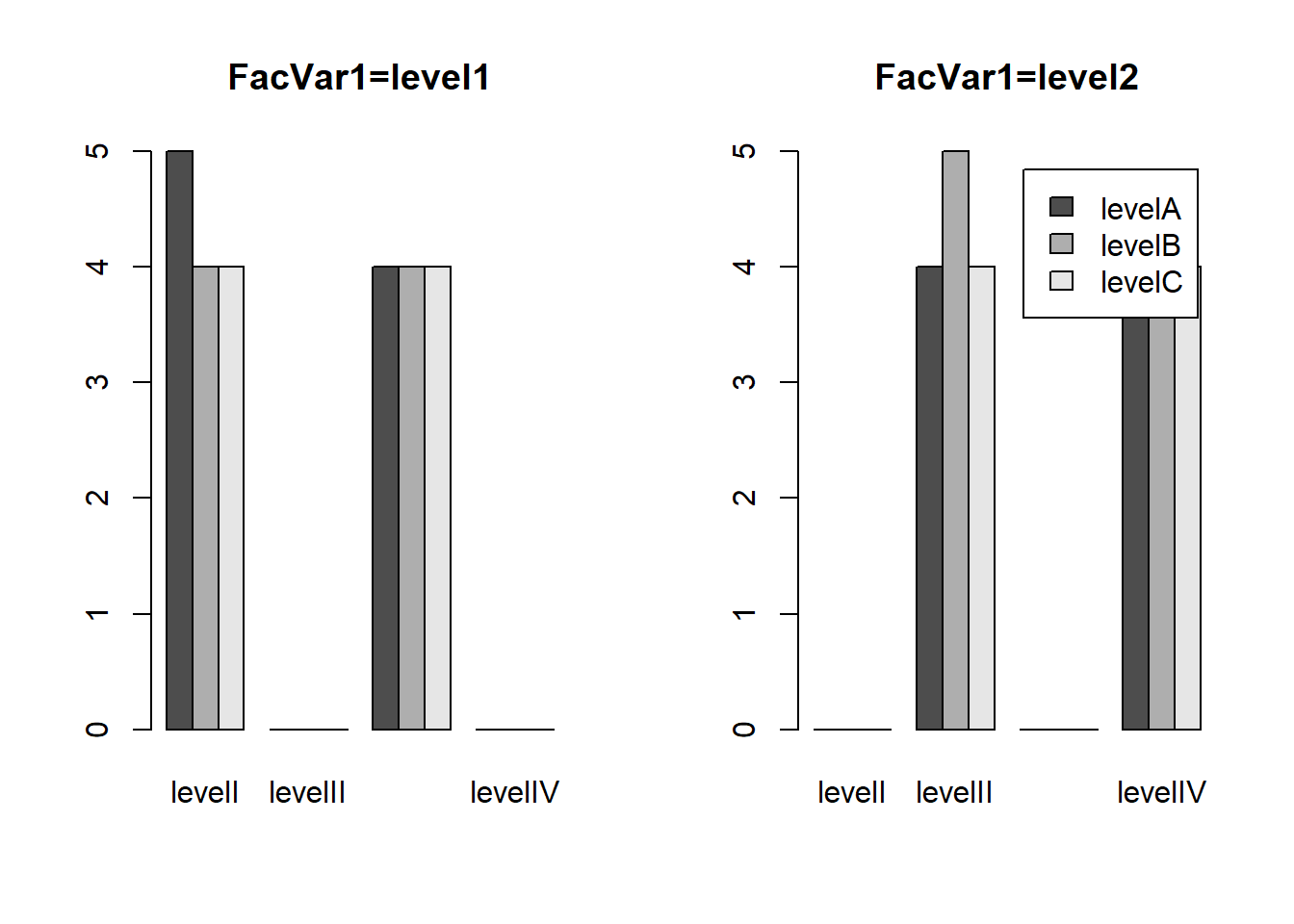

par(mfrow = c(1,1)) #retornando ao normal

8.10 Três Variáveis: Uma númérica e duas categóricas

8.10.1 Boxplot considerando a interação entre as duas variáveis categóricas

Considerando que cada variável aleatória tem 3 categorias, existem seis pares possíves, cada um podendo influenciar a variável contínua de maneira distinta.

boxplot(NumVar1 ~ interaction(FacVar1, FacVar2), data = simData)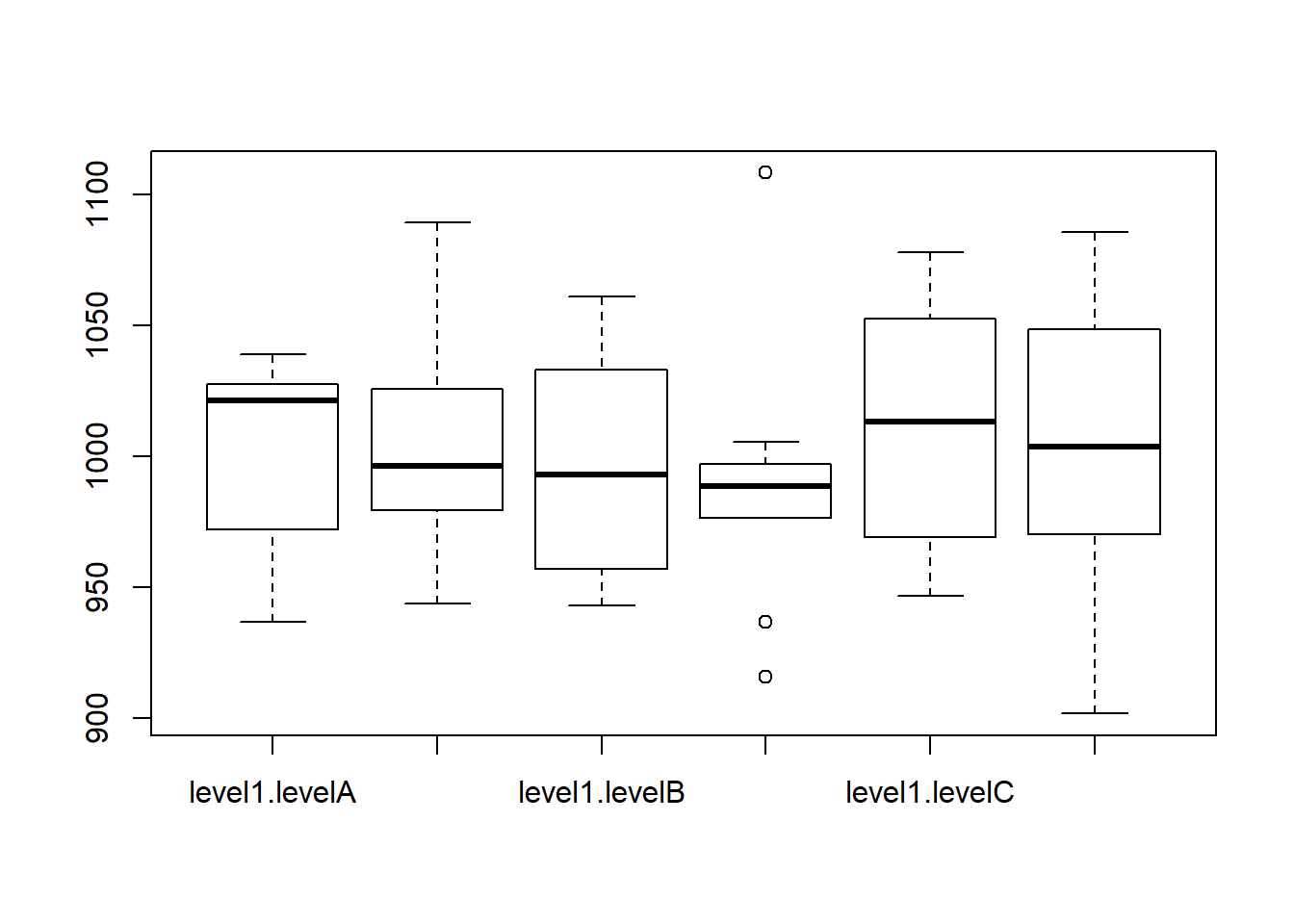

8.10.2 Média da variável numérica para cada par de interação das variáveis categóricas

meanaggg = aggregate(simData$NumVar1, list(simData$FacVar1, simData$FacVar2), 
    mean)
meanaggg = meanaggg[order(meanaggg$Group.1), ]
meanaggg$color[meanaggg$Group.2 == "levelA"] = "red"
meanaggg$color[meanaggg$Group.2 == "levelB"] = "blue"
meanaggg$color[meanaggg$Group.2 == "levelC"] = "darkgreen"
meanaggg
##   Group.1 Group.2         x     color
## 1  level1  levelA 1004.8489       red
## 3  level1  levelB  996.3175      blue
## 5  level1  levelC 1011.7713 darkgreen
## 2  level2  levelA 1004.5125       red
## 4  level2  levelB  989.9144      blue
## 6  level2  levelC 1004.0450 darkgreen
dotchart(meanaggg$x, labels = meanaggg$Group.2, groups = meanaggg$Group.1, color = meanaggg$color)  ## dotchart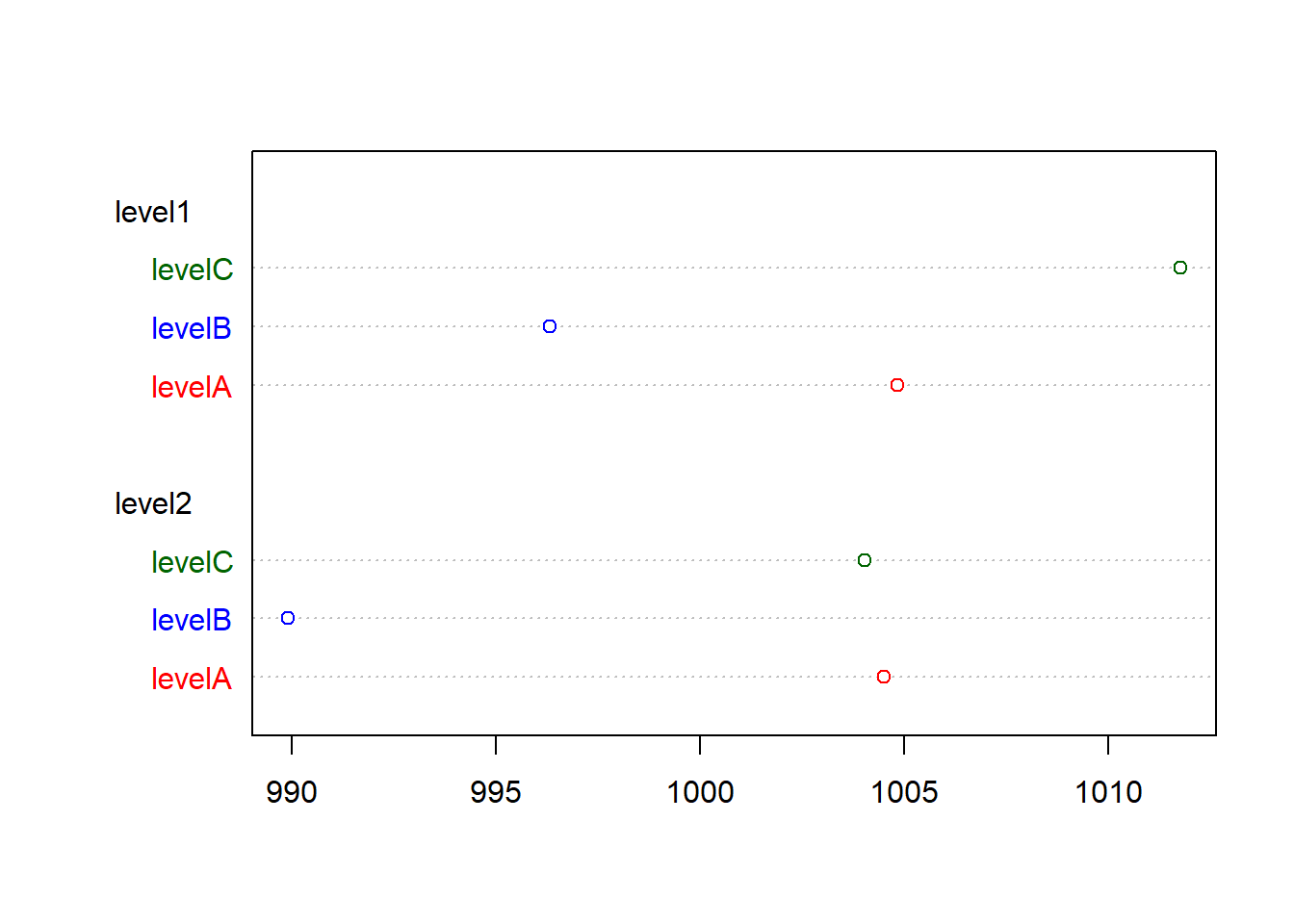

8.10.3 Gráfico de interação (interaction plot)

Uma categoria eixo x e a outra no símbolo utilizado.

interaction.plot(meanaggg$Group.2, meanaggg$Group.1, meanaggg$x, type = "b",
                 col = c(1:2), pch = c(18, 24))  ## interaction plot - line plots of means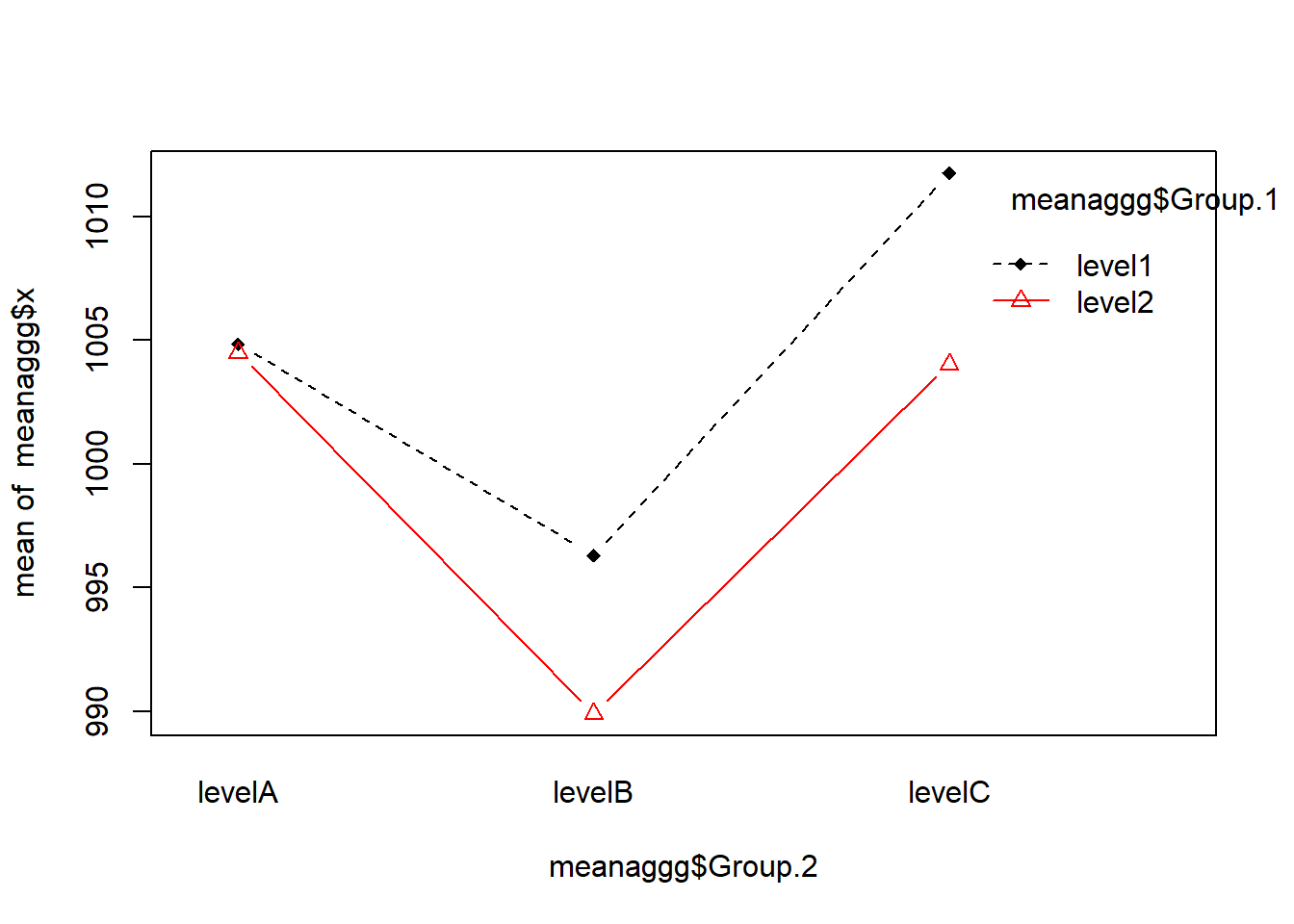

8.10.4 Gráfico de barras

Veja a dificuldade de identificar tais variações em um gráfico de barras

par(mfrow = c(1, 2))
meanaggg
##   Group.1 Group.2         x     color
## 1  level1  levelA 1004.8489       red
## 3  level1  levelB  996.3175      blue
## 5  level1  levelC 1011.7713 darkgreen
## 2  level2  levelA 1004.5125       red
## 4  level2  levelB  989.9144      blue
## 6  level2  levelC 1004.0450 darkgreen
level1 = meanaggg[meanaggg$Group.1 == "level1", ]
level2 = meanaggg[meanaggg$Group.1 == "level2", ]

barplot(level1$x, names.arg = level1$Group.2, main = "FacVar1=level1")
barplot(level2$x, names.arg = level2$Group.2, main = "FacVar1=level2")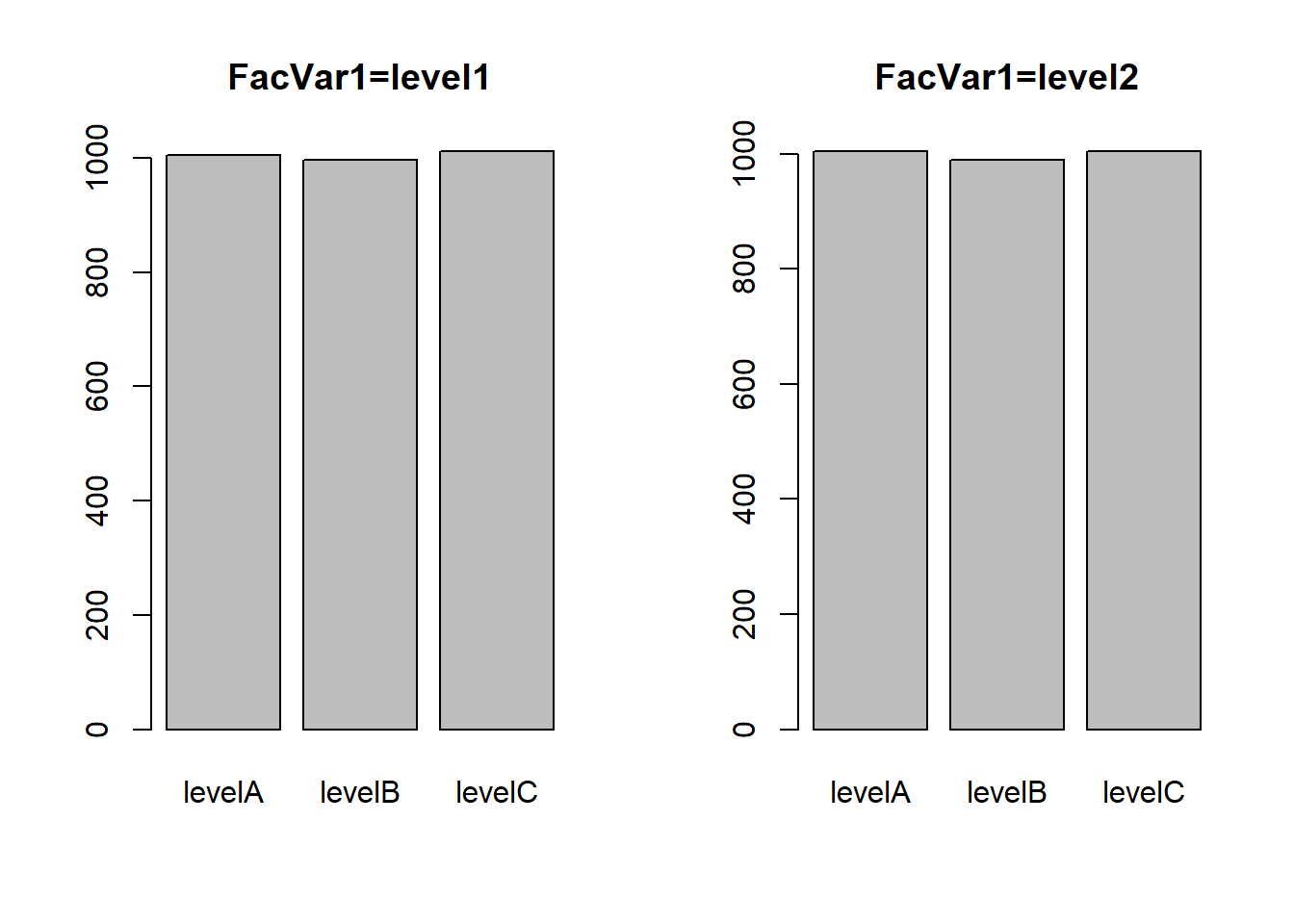

par(mfrow = c(1, 1))

8.11 Três variáveis: Duas numéricas e uma variável categórica

8.11.1 Gráfico de pontos usando cor

Aqui a cor é utilizada para identificar o valor da variável categorica

plot(simData$NumVar1, simData$NumVar2, col = simData$FacVar1)
legend("topright", levels(simData$FacVar1), fill = simData$FacVar1)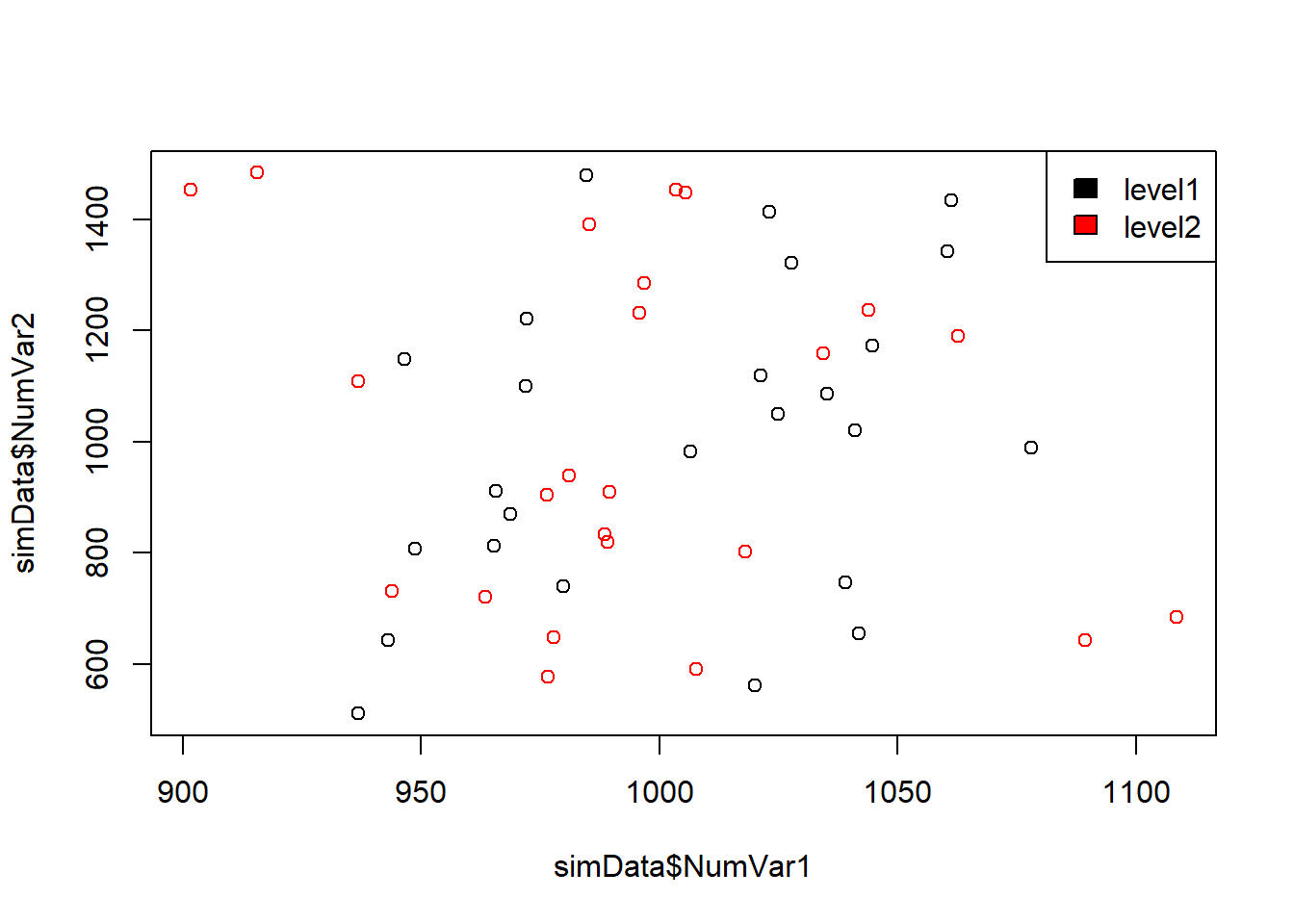

#Usando pontos sólidos para melhorar a visiualização
plot(simData$NumVar1, simData$NumVar2, col = simData$FacVar1, pch = 19)
legend("topright", levels(simData$FacVar1), fill = simData$FacVar1)

8.12 Três variáveis numéricas

8.12.1 Gráficos de Linhas

Considerando que NumVar4 varia de 2001 até 2050, vamos assumir que a mesma representaria uma data aque será usada no eixo x

plot(simData$NumVar4, simData$NumVar1, type = "o",
     ylim = c(0, max(simData$NumVar1, simData$NumVar2)))  ## join dots with lines

lines(simData$NumVar4, simData$NumVar2, type = "o", lty = 2, col = "red")  ## add another line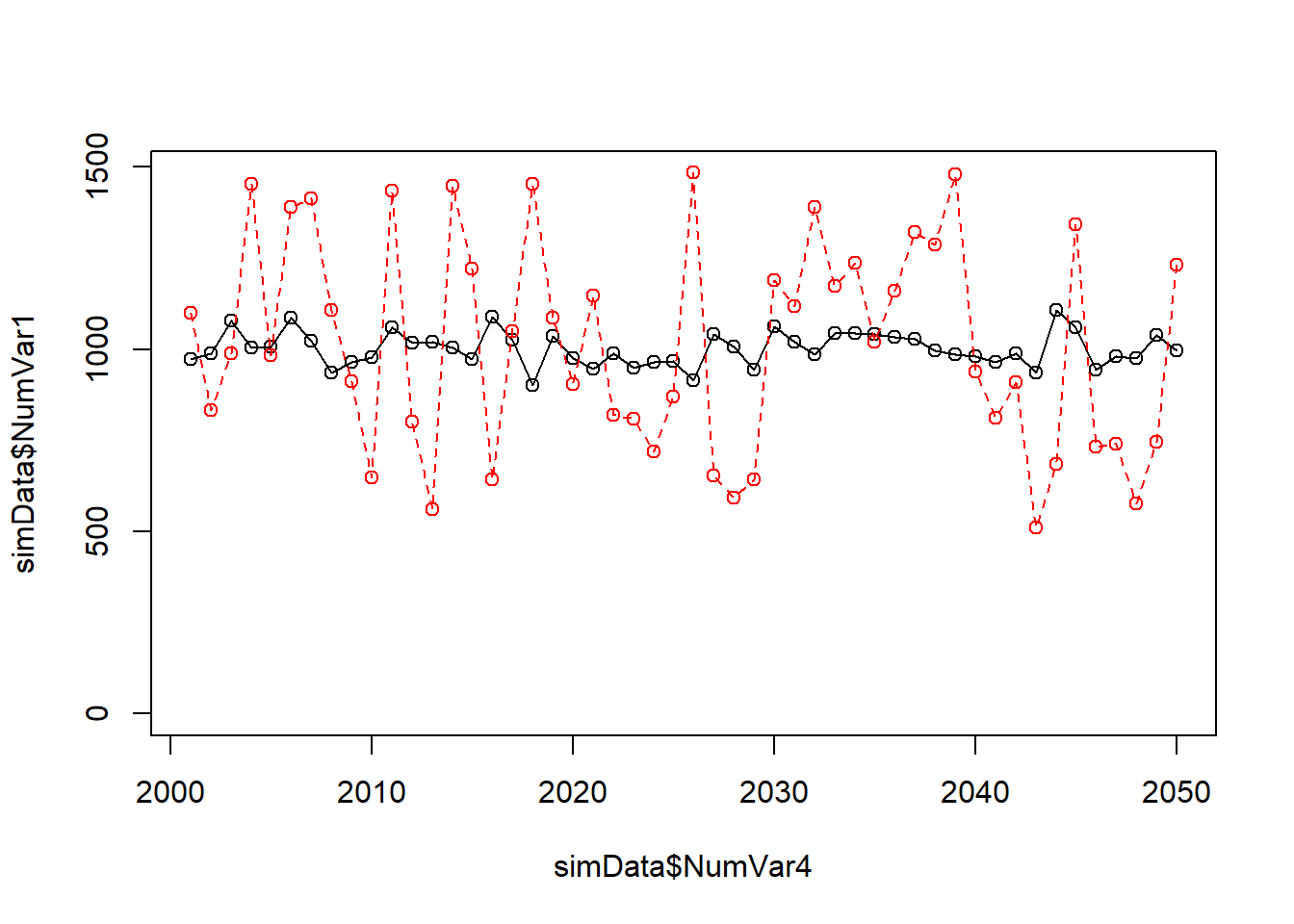

Observe que lines() permite que a gráfico poderá ser montado em níveis. Essa é uma funcionalidade muito útil, mas ainda limitada no sistema de gráficos do pacote básico. Veremos mais adiante um pacote mais poderoso implementado para explorar melhor esta possibilidade.

8.12.2 Gráfico de bolhas2

Esse é um gráfico que incorpora nos pontos definidos pelas variáveis NumVar1 and NumVar2 a informação da variável NumVar3, usando seu valor para definir o tamanho do ponto a ser plotado.

radius <- sqrt(simData$NumVar3/pi)
symbols(simData$NumVar1, simData$NumVar2, circles = radius, inches = 0.25, fg = "white", 
    bg = "red", main = "Tamanho dado por NumVar3")

8.12.3 Gráfico de pares

Finalmente, um gráfico de pontos (Scatterplot) na forma de uma matriz simétrica que apresenta a correlação espacial entre os pares das variáveis numéricas, coloridas por uma variável discreta.

pairs(simData[, 4:7], col = simData$FacVar1, pch = 19)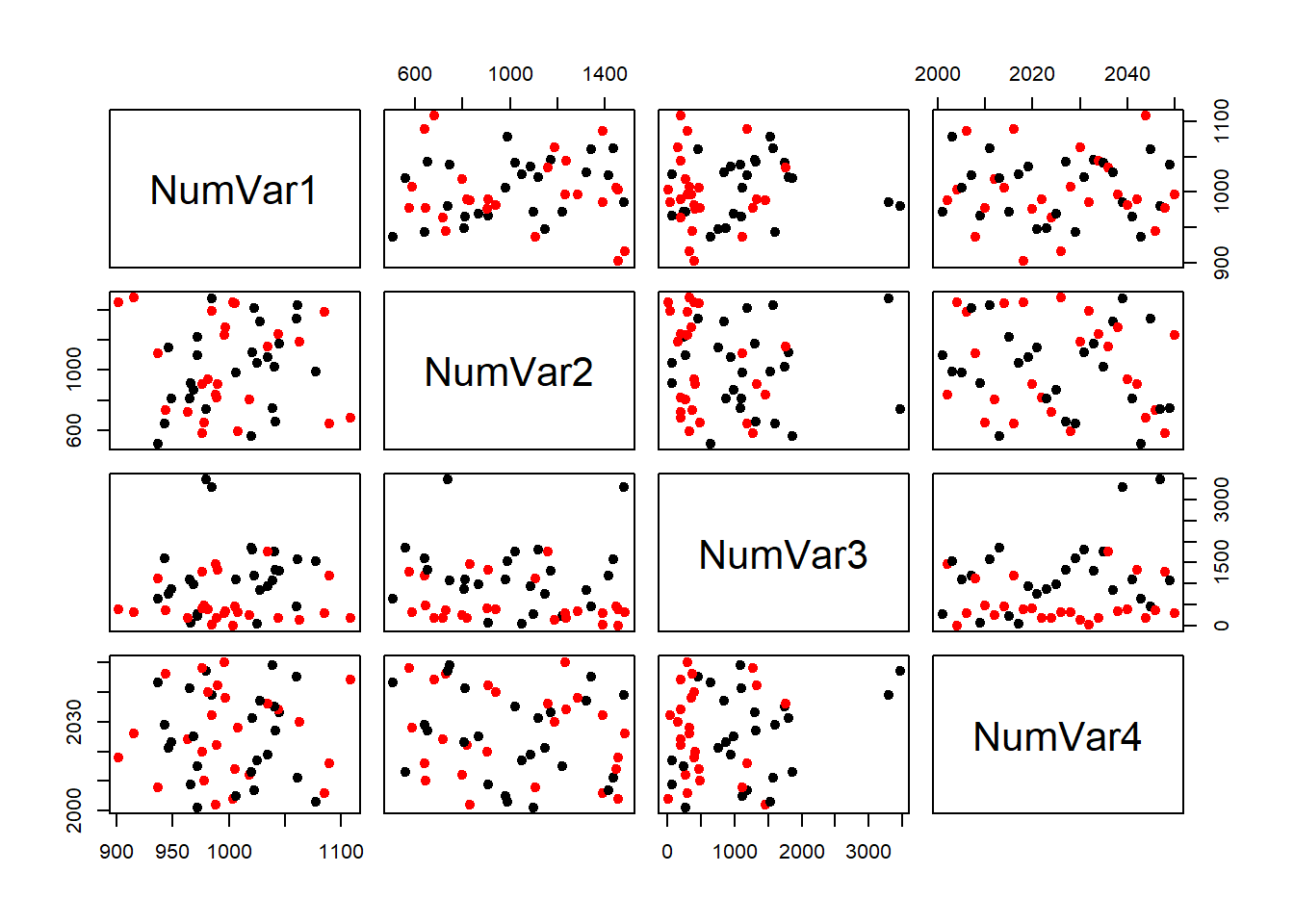

Na verdade, a medida que vamos incrementando a apresentação de mais informações nos gráficos, os comandos passam a ganhar maior complexidade quando usamos apenas o pacote base. No próximo capítulo veremos um pacote especialmente implementado para lidar com essa problemática, facilitado em muito a criação de gráficos mais informativos.

References

Matejka, Justin, and George Fitzmaurice. 2017. “Same Stats, Different Graphs.” Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems - CHI ’17, 1290–4. doi:10.1145/3025453.3025912.

  1. Esse conteúdo foi adaptado do site http://bl.ocks.org/patilv/raw/7360425/.↩

  2. http://flowingdata.com/2010/11/23/how-to-make-bubble-charts/↩